1. OOP
1-1. 객체지향의 4가지 특성
a. 다형성
한 가지 역할이 상황에 따라 각기 다른 행동을 한다.
- 셰프가 헛기침을_한다()
- 부 주방장 -> 눈치를_본다()
- 조리장 -> 요리하는_척을_한다()
b. 추상화
- 공통된 기능을 뽑아낸다.
- 현실 세계의 복잡한 현상을 간단한 형태로 모델링한다. (simplify)
최소한의 정보를 추출
c. 캡슐화
- 구현 내용을 내부에 숨겨서 응집도를 높이는 것
- 응집도 : 객체가 자신과 관련된 것을 중심적으로 행동한다.
c-1. 결합도
- 두 객체가 서로 관련되거나 의존하는 정도
- 안 좋은거 (객체를 떼어내거나 변경하기 힘들다)
c-2. 캡슐화를 위반한 사례
- 신문배달부가 고객의 지갑을 가져와서, 현금을 확인하고, 돈을 가져가는게 아니라
- 고객이 자신의 지갑의 현금을 확인하고, 돈을 신문배달부에게 건네주는 것
d. 상속
- 부모의 기존 기능을 물려받을 수 있다.
1-2. SOLID
좋은 객체 지향 설계를 위한 5가지 원칙
a. Single-Responsibility Principle (단일 책임 원칙)
- 객체는 오로지 하나의 책임을 갖는다
- 공통된 일을 하는 객체를 하나 둠으로써, 중복된 코드를 최대한 제거한다.
b. Open/Closed Principle (개방/폐쇄 원칙)
- 변경에는 닫혀있고 확장에는 열려있다.
- 클라이언트 코드가 바뀌지 않도록 한다.
- 부모 class에서 자식 class를 만들 때, 자식 class에서 기능을 추가/수정할 수 있지만,
자식 class를 위해 부모 class가 수정될 필요는 없다.
c. Liskov’s Substitution Principle (리스코프 치환 원칙)
- 상위 타입을 하위 타입으로 바꾸더라도 정상 작동해야 한다.
- Ex. 정사각형에 직사각형의 속성을 상속을 받는 순간 정사각형의 성질에 위배된다.
- 부모 class의 위치에 자식 class로 넣어도 어떠한 issue도 없어야 한다는 원칙이다.
d. Interface Segregation Principle (인터페이스 분리 원칙)
- 클라이언트 입장에서 필요한 기능 중심으로 인터페이스를 분리한다.
- 클라이언트가 자신과 관련이 없는 인터페이스는 구현하지 않아야 한다.
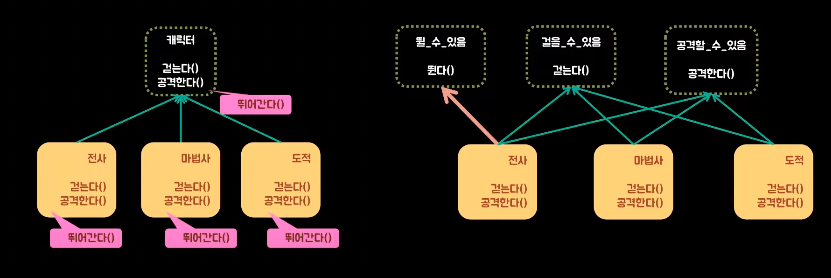
e. Dependency Inversion Principle (의존성 역전 법칙)
- 저수준 모듈이 고수준 모듈에서 정의한 추상 타입에 의존해야 한다.
- -> 부모 class는 자식 class에 의존해서는 안된다.
- 클라이언트 입장에서 필요한 인터페이스를 추출한다.
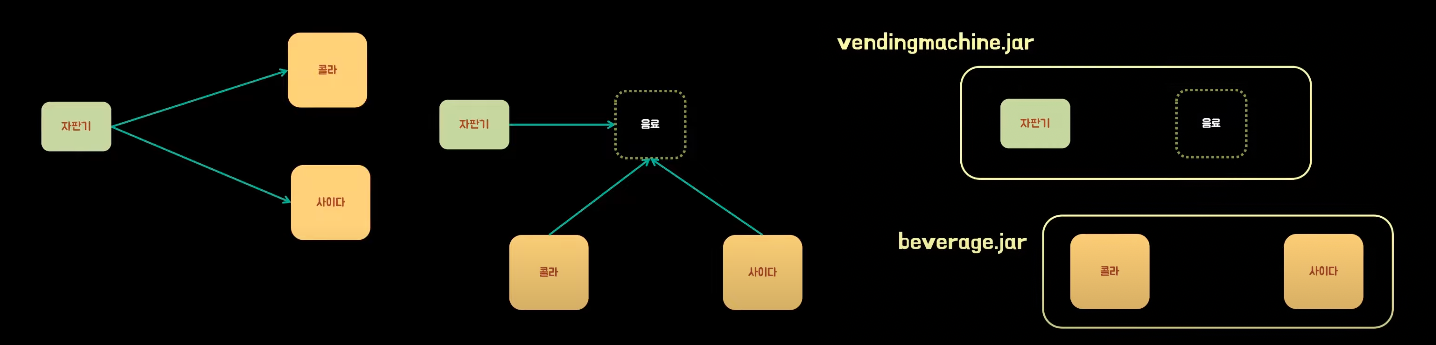
- 독립배포가 가능해진 다는 장점
2. FP
a. Pure Function (순수함수)
- 같은 입력값에는 같은 결과값을 반환한다.
- 그러면서 side effect가 없는 것.
return 2*xvsalpha = x; return 2*alpha: 전자가 순수함수
b. Immutability (불변성)
- 이미 저장된 값의 상태를 변경하지 않는다.
- oop에서는 Private, Public 등의 접근 제어자로 통제를 할 수 있지만, FP는 기본적으로 아무런 내부 상태를 변화시키지 않는다.
- 데이터의 변경이 필요한 경우, 그 데이터의 복사본을 만들어 변경하고, 해당 복사본을 사용해 작업한다.
c. Declerative Pattern (선언적 패턴)
- How 보다는 What에 집중한다.
// 명령형 프로그래밍. 어떻게 수행할지
let numbers = [1, 2, 3];
function multiply(numbers, multiplier) {
for (let i = 0; i < numbers.length; i++) {
numbers[i] = numbes[i] * multiplier;
}
}// 함수형 프로그래밍. 무엇을 수행할지
function multiply(number, multiplier) {
return number.map((num) => num * multiplier);
}- Map, filter 등등이 함수형 코드라고 함
d. First Class Function (1급 객체)
함수형 프로그래밍에선 함수를 1급 객체로 취급한다.
- 변수나 데이터 구조 안에 담을 수 있고, 파라미터나 반환값으로 사용할 수 있다.
- 아직 자바에선 함수를 1급 객체로 취급하진 않음
// 1급 객체
const addTwo = (num) => num + 2;
const multiplyTwo = (num) => num * 2;
const transform = (numbers) => numbers.map(addTwo).map(multiplyTwo);
console.log(transform([1, 2, 3, 4])); // [6, 8, 10, 12]
e. High Order Function (고차함수)
- 함수를 함수의 인자로 받는다.
- 함수의 반환값으로 또 다른 함수를 사용한다.
const func1 = (func) => (word) => {
func();
console.log(`${word}`);
};
e.1 커링(currying) 기법
- 인자가 여러개인 함수의 일부 인자를 고정시키는 새로운 함수를 만드는 기법
function helloFunc(word) {
return function (name) {
console.log(`${word}, ${name}`);
};
}
const printHello = helloFunc("hello");
printHello("Tibetan Fox"); // hello, Tibetan Fox
printHello("Tiger"); // hello, Tiger- 커링 기법은 일부 인자에 같은 값을 반복적으로 사용할 때 그 반복되는 인자를 고정함으로써 중복을 최소화 하기에 적합한 기법
함수형 프로그래밍
- 프로그래밍 패러다임 중 하나
- 순수 함수를 통해서 어플리케이션의 상태가 흐른다
- 병렬 처리의 장점을 가진다 (순수함수->부수효과가 없다. 즉, 스레드에 안정성 보장)
- 간결하고 재사용성이 높다
